[Leetcode] 5. Longest Palindromic Substring (Manacher's Algorithm)

Table of Contents

Description

Given a string s, return the longest palindromic substring in s.

Example 1:

Input: s = “babad”
Output: “bab”
Explanation: “aba” is also a valid answer.

Example 2:

Input: s = “cbbd”
Output: “bb”

Constraints:

• 1 <= s.length <= 1000
• s consist of only digits and English letters.

Approach

We previously used the expand-around-center (two-pointer) technique to solve this problem 👉 Solution.

However, we can solve this problem using Manacher’s Algorithm. This algorithm employs center expansion with additional bookkeeping to efficiently find the longest palindromic substring in $O(n)$.

Let’s explore how it works and how it differs from the previous solution.

Previous Solution (Expand Around Center)

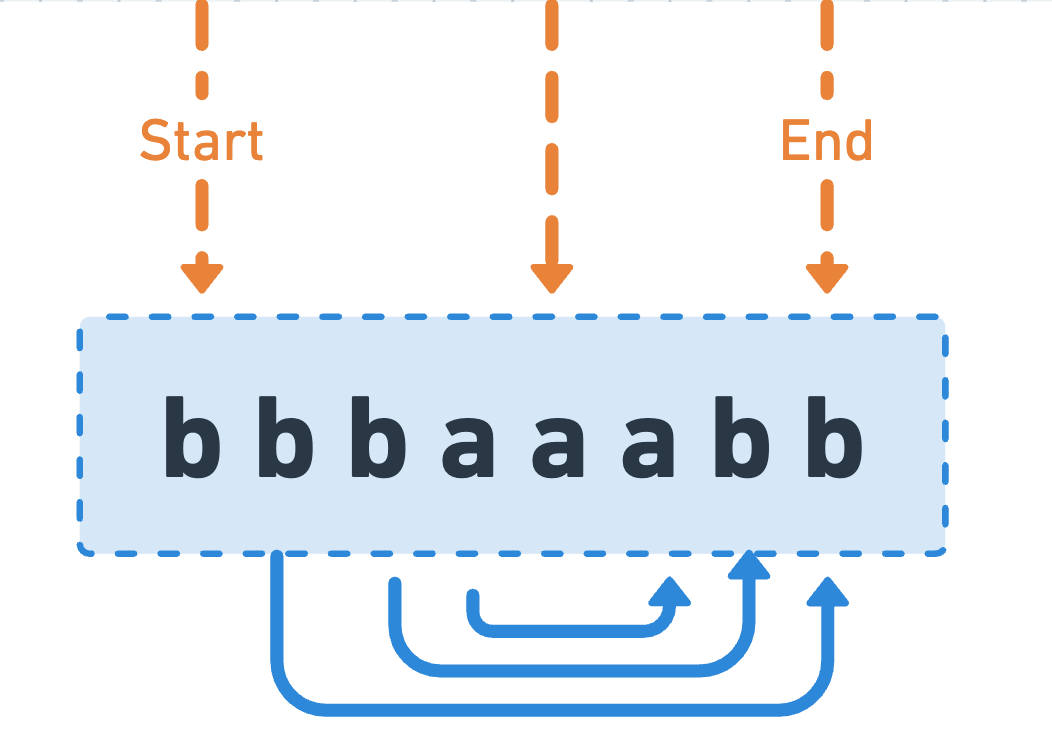
We traverse the string from start to end, treating each character and the gap between characters as centers. From each center, we expand outward to find the longest palindromic substring.

Since we expand around every character and gap, the time complexity is $O(n^2)$

/**
 * @param {string} s
 * @return {string}
 */
var longestPalindrome = function (s) {
  // Transform input string by inserting '_' between characters and at both ends
  // Example: "babad" -> "_b_a_b_a_d_"
  const transformedString = `_${s.split("").join("_")}_`;
  const palindromeLengths = new Array(transformedString.length).fill(0);

  let maxCenterIndex = 0; // center index of the longest palindrome found
  let maxLength = 0; // radius of the longest palindrome found

  for (
    let centerIndex = 0;
    centerIndex < transformedString.length;
    centerIndex++
  ) {
    // Expand around centerIndex while characters on both sides are equal
    for (
      let left = centerIndex - 1, right = centerIndex + 1;
      right < transformedString.length &&
      transformedString[left] === transformedString[right];
      left--, right++, palindromeLengths[centerIndex]++
    ) {}

    // Update max palindrome info if current one is longer
    if (palindromeLengths[centerIndex] > maxLength) {
      maxLength = palindromeLengths[centerIndex];
      maxCenterIndex = centerIndex;
    }
  }

  // Extract the longest palindrome substring from the transformed string,
  // then remove all '_' separators to get the original palindrome
  return transformedString
    .slice(maxCenterIndex - maxLength, maxCenterIndex + maxLength)
    .replaceAll("_", "");
};

Solution (Manacher’s Algorithm)

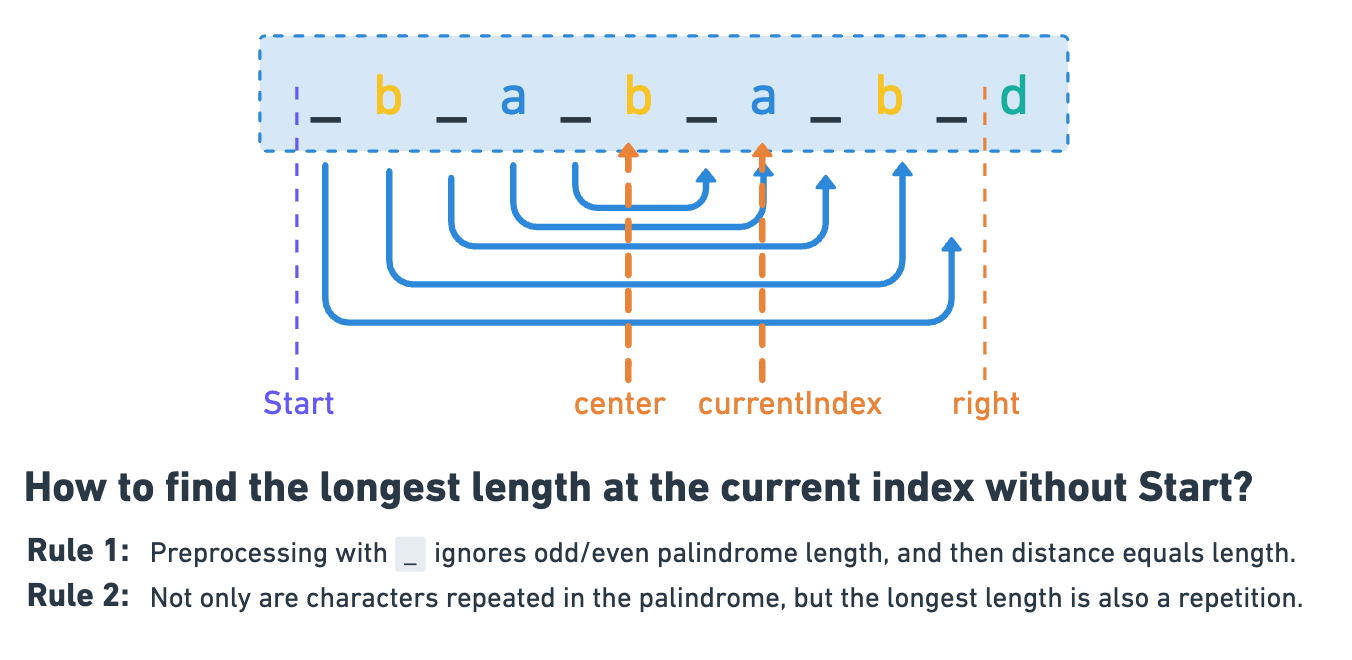
Manacher’s Algorithm improves upon the previous approach by maintaining a center and right for the current rightmost palindrome. It uses this information to skip unnecessary checks and efficiently expand palindromes.

/**
 * @param {string} s
 * @return {string}
 */
var longestPalindrome = function (s) {
  // Transform input string by inserting '_' between characters and at both ends
  // Example: "babad" -> "_b_a_b_a_d_"
  const transformedString = `_${s.split("").join("_")}_`;
  const palindromeLengths = new Array(transformedString.length).fill(0);

  let center = 0; // center of the current rightmost palindrome
  let right = 0; // right boundary of the current rightmost palindrome
  let maxCenterIndex = 0; // center index of the longest palindrome found
  let maxLength = 0; // radius of the longest palindrome found

  for (
    let currentIndex = 0;
    currentIndex < transformedString.length;
    currentIndex++
  ) {
    // Mirror position of currentIndex with respect to center
    const mirrorIndex = 2 * center - currentIndex;

    // If currentIndex is within the right boundary, use the mirror's palindrome radius or distance to boundary
    if (currentIndex < right) {
      palindromeLengths[currentIndex] = Math.min(
        palindromeLengths[mirrorIndex],
        right - currentIndex
      );
    }

    // Expand around centerIndex while characters on both sides are equal
    while (
      currentIndex + palindromeLengths[currentIndex] + 1 <
        transformedString.length &&
      currentIndex - palindromeLengths[currentIndex] - 1 >= 0 &&
      transformedString[currentIndex + palindromeLengths[currentIndex] + 1] ===
        transformedString[currentIndex - palindromeLengths[currentIndex] - 1]
    ) {
      palindromeLengths[currentIndex]++;
    }

    // If palindrome expanded beyond right, update center and right
    if (currentIndex + palindromeLengths[currentIndex] > right) {
      center = currentIndex;
      right = currentIndex + palindromeLengths[currentIndex];
    }

    // Track the longest palindrome found so far
    if (palindromeLengths[currentIndex] > maxLength) {
      maxLength = palindromeLengths[currentIndex];
      maxCenterIndex = currentIndex;
    }
  }

  // Extract the longest palindrome substring from the transformed string,
  // then remove all '_' separators to get the original palindrome
  return transformedString
    .slice(maxCenterIndex - maxLength, maxCenterIndex + maxLength)
    .replaceAll("_", "");
};

Complexity Analysis

Time Complexity

The time complexity for Manacher’s Algorithm is $O(n)$ because it preprocesses the string and then finds the longest palindromic substring using a linear scan with center expansion.

Space Complexity

The space complexity for Manacher’s Algorithm is $O(n)$ due to the array palindromeLengths used for storing the lengths of palindromes centered at each position in the transformed string.