[LeetCode] 70. Climbing Stairs

Table of Contents

Description

You are climbing a staircase. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Example 1:
Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

Example 2:
Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

Approach

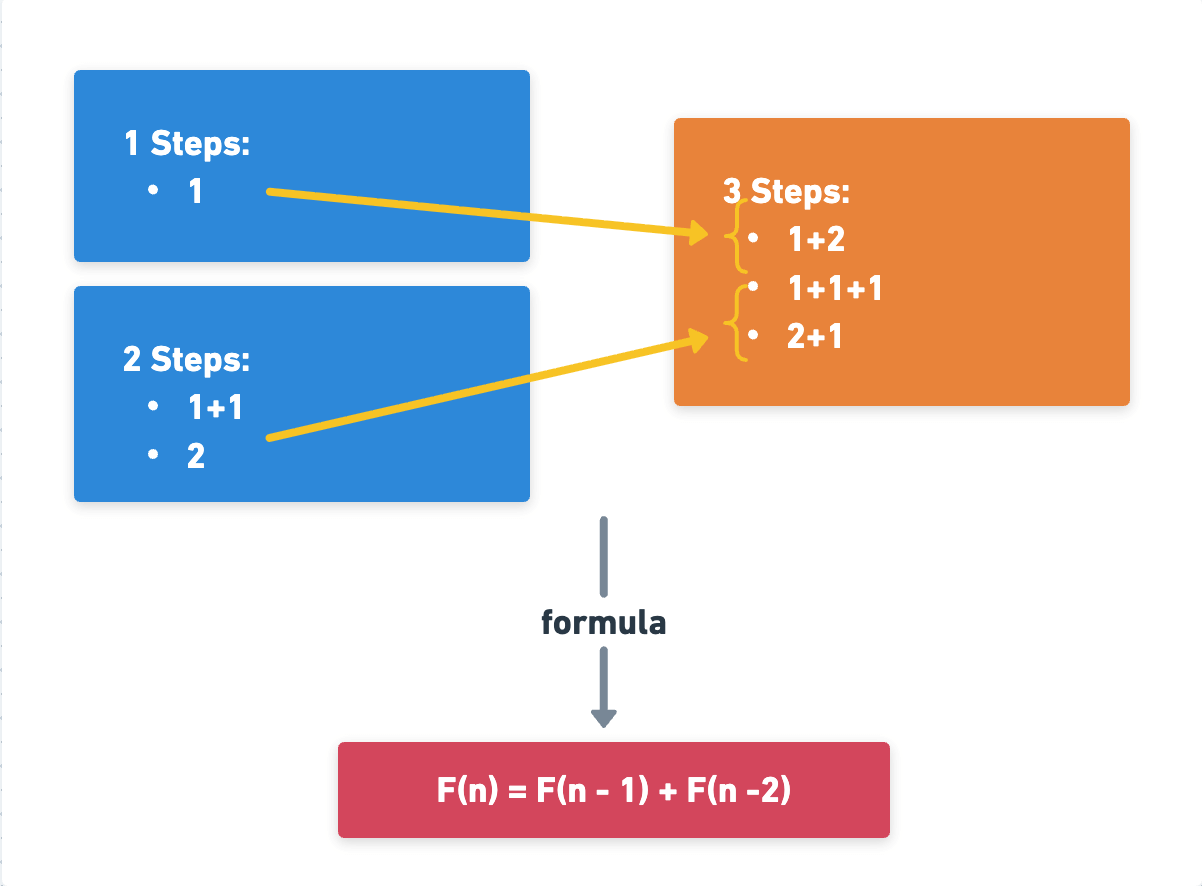
We can use a dynamic programming approach. The key observation is that to reach the i-th step, you could have come from either the (i-1)-th step (by taking a single step) or the (i-2)-th step (by taking a double step).

Therefore, the number of ways to reach the i-th step can be expressed as: $\text{ways}(i) = \text{ways}(i-1) + \text{ways}(i-2)$

Solution

/**
 * @param {number} n
 * @return {number}
 */
var climbStairs = function (n) {
  // numWaysToClimb[i] stores the number of ways to climb 'i' steps.
  // Base cases: 0 steps (placeholder), 1 step (1 way), 2 steps (2 ways).
  // numWaysToClimb[1]: 1 way to climb 1 step (take one 1-step).
  // numWaysToClimb[2]: 2 ways to climb 2 steps (take two 1-steps: 1+1, or take one 2-step: 2).
  const numWaysToClimb = [0, 1, 2];

  // For each step 'i', the ways to reach it are the sum of ways to reach (i-1) and (i-2).
  for (let i = numWaysToClimb.length; i <= n; i++) {
    numWaysToClimb[i] = numWaysToClimb[i - 1] + numWaysToClimb[i - 2];
  }

  return numWaysToClimb[n];
};

Complexity Analysis

Time Complexity

The time complexity is $O(n)$ because we use a single loop that iterates up to n, calculating the number of ways to climb each step.

Space Complexity

The space complexity is $O(n)$ due to the array numWaysToClimb that stores the number of ways to climb each step up to n.