[LeetCode] 42. Trapping Rain Water

Table of Contents

Description

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.

Example 1:

Input:

height = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1];

Output: 6
Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.

Example 2:

Input:

height = [4, 2, 0, 3, 2, 5];

Output: 9

Constraints:

• $n = \text{height.length}$
• $0 \leq n \leq 2 \times 10^4$
• $0 \leq \text{height}[i] \leq 10^5$

Approach

To determine trapped water above each bar, calculate the minimum of maximum heights to its left and right, then subtract the bar’s height. Iterate through the array to compute water trapped at each position.

$\text{total} = \sum_{i=0}^{n-1} \max\left(0, \min(\text{maxLeft}_i, \text{maxRight}_i) - h_i \right)$

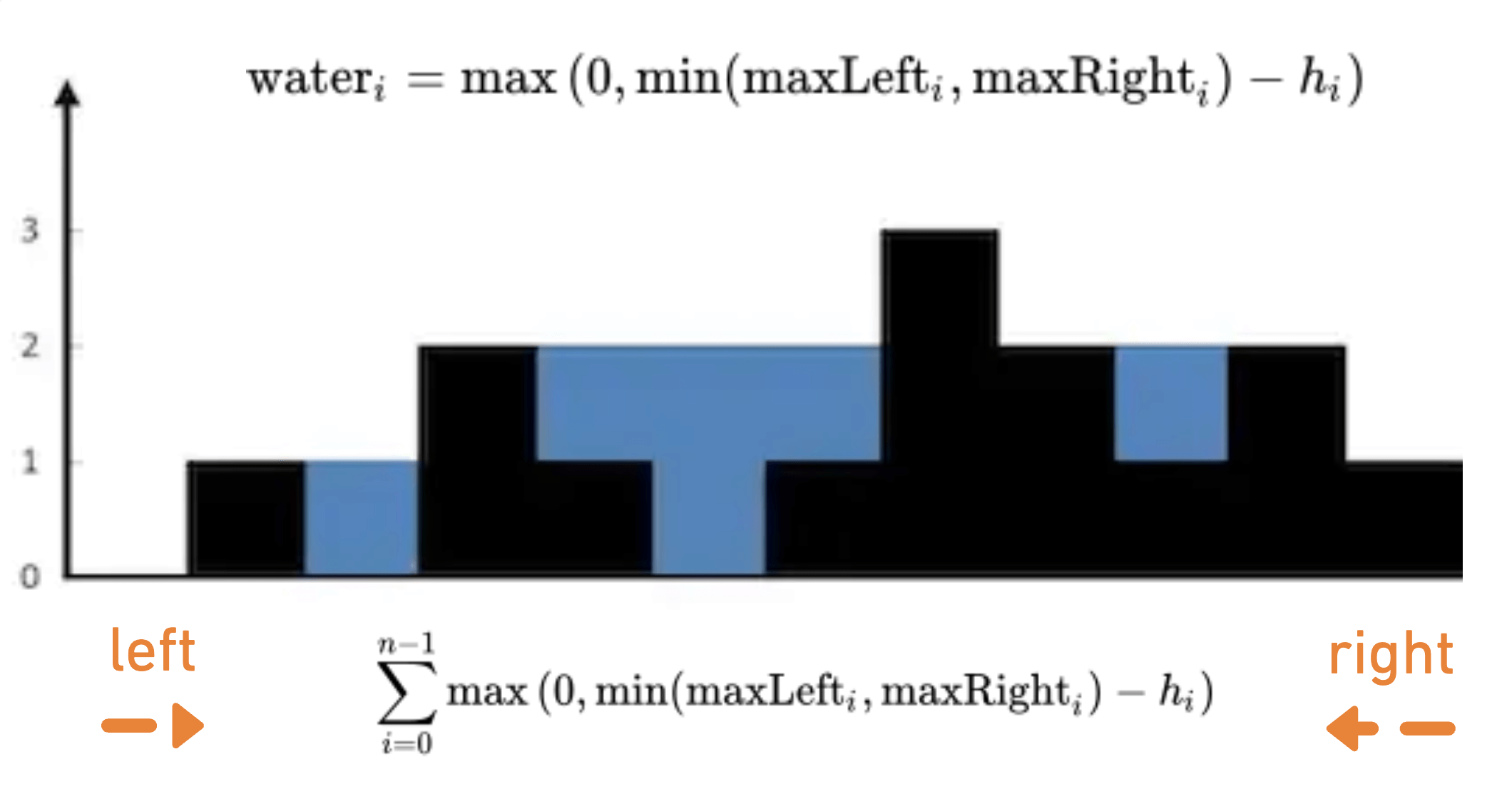
Solution 1

However, this approach has a time complexity of $O(n^2)$ because for each position, it traverses the array to find the maximum heights on the left and right. As a result, this solution is usually too slow and will exceed the time limit in actual submission.

/**
 * @param {number[]} height
 * @return {number}
 */
var trap = function (height) {
  let total = 0;

  // Iterate through each position in the height array
  for (let i = 0; i < height.length; i++) {
    // Find the highest bar to the left of the current position (excluding current)
    const maxLeftHeight = Math.max.apply(null, height.slice(0, i));
    // Find the highest bar to the right of the current position (excluding current)
    const maxRightHeight = Math.max.apply(null, height.slice(i + 1));

    // Calculate trapped water at position i:
    // Minimum of the highest bars on left and right minus current height,
    // but not less than 0 (no negative water)
    total += Math.max(Math.min(maxLeftHeight, maxRightHeight) - height[i], 0);
  }

  return total;
};

Solution 2

We can solve Trapping Rain Water in (O(n)) time using two pointers at array ends, tracking maximum heights from left and right. By comparing current heights and moving pointers inward, we calculate trapped water efficiently with constant extra space.

/**
 * @param {number[]} height
 * @return {number}
 */
var trap = function (height) {
  let maxLeft = 0,
    maxRight = 0,
    total = 0;
  let left = 0,
    right = height.length - 1;

  while (left < right) {
    // Compare heights at left and right pointers
    if (height[left] < height[right]) {
      // If current left height is greater or equal to maxLeft, update maxLeft
      if (height[left] >= maxLeft) {
        maxLeft = height[left];
      } else {
        // Otherwise, water can be trapped on top of current left bar
        total += maxLeft - height[left];
      }
      left++;
    } else {
      // If current right height is greater or equal to maxRight, update maxRight
      if (height[right] >= maxRight) {
        maxRight = height[right];
      } else {
        // Otherwise, water can be trapped on top of current right bar
        total += maxRight - height[right];
      }
      right--;
    }
  }

  return total;
};

Complexity Analysis

Time Complexity

• Solution 1 (Brute Force):

  • Time complexity is $O(n^2)$, where $n$ is the length of the array. For each bar, we scan all bars to its left and right to find the maximum heights.

• Solution 2 (Two Pointers):

  • Time complexity is $O(n)$, where $n$ is the length of the array. Each index is visited at most once as the left and right pointers move toward each other.

Space Complexity

Both solutions have a space complexity of $O(1)$, as they only use a constant amount of extra variables regardless of the input size.