[LeetCode] 36. Valid Sudoku

Table of Contents

Description

Determine if a 9x9 Sudoku board is valid. Only the filled cells need to be validated according to the following rules:

• Each row must contain the digits 1-9 without repetition.
• Each column must contain the digits 1-9 without repetition.
• Each of the nine 3x3 sub-boxes must contain the digits 1-9 without repetition.

Note:

• A Sudoku board (partially filled) could be valid but is not necessarily solvable.
• Only the filled cells need to be validated according to the above rules.

Example 1:

Input:

board = [
  ["5", "3", ".", ".", "7", ".", ".", ".", "."],
  ["6", ".", ".", "1", "9", "5", ".", ".", "."],
  [".", "9", "8", ".", ".", ".", ".", "6", "."],
  ["8", ".", ".", ".", "6", ".", ".", ".", "3"],
  ["4", ".", ".", "8", ".", "3", ".", ".", "1"],
  ["7", ".", ".", ".", "2", ".", ".", ".", "6"],
  [".", "6", ".", ".", ".", ".", "2", "8", "."],
  [".", ".", ".", "4", "1", "9", ".", ".", "5"],
  [".", ".", ".", ".", "8", ".", ".", "7", "9"],
];

Output: true

Example 2:

Input:

board = [
  ["8", "3", ".", ".", "7", ".", ".", ".", "."],
  ["6", ".", ".", "1", "9", "5", ".", ".", "."],
  [".", "9", "8", ".", ".", ".", ".", "6", "."],
  ["8", ".", ".", ".", "6", ".", ".", ".", "3"],
  ["4", ".", ".", "8", ".", "3", ".", ".", "1"],
  ["7", ".", ".", ".", "2", ".", ".", ".", "6"],
  [".", "6", ".", ".", ".", ".", "2", "8", "."],
  [".", ".", ".", "4", "1", "9", ".", ".", "5"],
  [".", ".", ".", ".", "8", ".", ".", "7", "9"],
];

Output: false
Explanation: Same as Example 1, except with the 5 in the top left corner being 8. Since there are two 8. Since there are two 8s in the top left 3x3 sub-box, it is invalid.

Approach

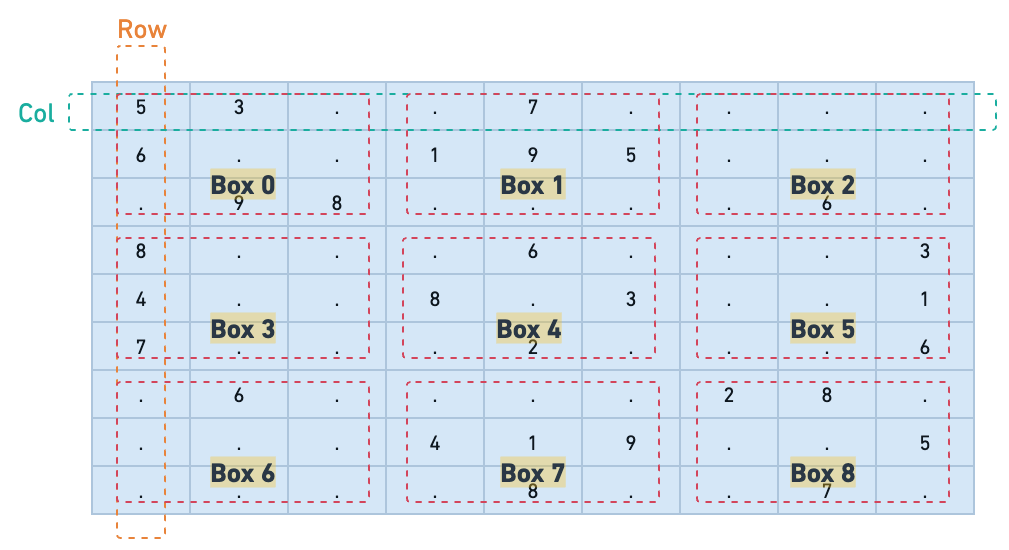
To solve the problem of validating a Sudoku board, we can use a set to track the numbers seen in each row, col, and 3x3 box. The algorithm iterates through each cell in the board, checking if the number is already present in the corresponding row, column, or sub-box. If a duplicate is found, the board is invalid.

Solution

/**
 * @param {character[][]} board
 * @return {boolean}
 */
var isValidSudoku = function (board) {
  const BOARD_SIZE = 9;
  const BOX_SIZE = 3;

  // Initialize arrays of Sets to track seen numbers in rows, columns, and boxes
  const rows = Array.from({ length: BOARD_SIZE }, () => new Set());
  const cols = Array.from({ length: BOARD_SIZE }, () => new Set());
  const boxes = Array.from({ length: BOARD_SIZE }, () => new Set());

  // Iterate through each cell in the board
  for (let row = 0; row < BOARD_SIZE; row++) {
    for (let col = 0; col < BOARD_SIZE; col++) {
      const val = board[row][col];

      // Skip empty cells denoted by '.'
      if (val === ".") continue;

      // Calculate box index based on row and column
      const boxIndex =
        Math.floor(row / BOX_SIZE) * BOX_SIZE + Math.floor(col / BOX_SIZE);

      // Check if the value has already been seen in the current row, column, or box
      if (
        rows[row].has(val) ||
        cols[col].has(val) ||
        boxes[boxIndex].has(val)
      ) {
        // Duplicate found, board is invalid
        return false;
      }

      // Mark the value as seen in the current row, column, and box
      rows[row].add(val);
      cols[col].add(val);
      boxes[boxIndex].add(val);
    }
  }

  // No duplicates found, board is valid
  return true;
};

Complexity Analysis

Time Complexity

The time complexity is $O(n^2)$, where $n$ is the size of the board (in this case, $9$). The algorithm iterates through each cell in the 9x9 board, performing constant-time operations for each cell. Since the board size is fixed, we can consider it a constant factor, leading to an overall time complexity of $O(1)$ for this specific problem.

Space Complexity

The space complexity is $O(n)$, where $n$ is the size of the board (in this case, $9$). We use three arrays of sets to track seen numbers in rows, columns, and boxes. Each set can contain at most $9$ unique numbers, leading to a constant space usage. Thus, the overall space complexity is also $O(1)$ for this specific problem.